A few weeks ago I was tweeting about the excellent Statistics in Medicine MOOC offered by Kristin Sainani of Stanford University when Ernesto asked:
@BoringEM how do you find this as a resident? Is statistics a gap in your training? #justcurious
— Ernesto (@DilettanteMD) July 22, 2013
Well, is it? I was taught statistics in medical school and my residency program incorporated them into its curriculum. However, I feel like I always “got by” rather than really learned statistics. I think this was at least in part because of my ambivalence and in part because I focused on the wrong things.
Over the next two posts I hope to convince a few (I’m aiming for 3!) medical students of the utility of statistics in clinical medicine and to distinguish between some of the more and less useful statistics. Due to length I’ve split this entry into diagnostic tests (post #1) and treatment statistics (post #2).
I know this is not the most exciting topic…
So it fits my website perfectly!
Diagnostic Statistics
What I thought would be useful: Sensitivity & Specificity
Sensitivity and specificity are the characteristics of diagnostic tests that I learned best in medical school. They were focused on in class and the most common calculations on exams. It made sense that we could adjust a laboratory tests positive/negative cut-offs to optimize one or both depending on these values and what we wanted the test to do (ie – screening tests often sacrifice specificity for sensitivity). After further training I think these measures are valuable characteristics to describe a test, but less useful in clinical practice.
Why? Because when I am using a test I do not know whether or not my patient has the disease!
Sensitivity =
How often the test is positive in patients WITH the disease
True Positive / (True Positive + False Negative)
a / (a + c)Specificity =
How often the test is negative in patients WITHOUT the disease
True Negative / (True Negative + False Positive)
d / (b + d)
It is difficult to make use of this information clinically because when we do a test we do not know whether the sensitivity matters (because the patient has the disease) or the specificity matters (because the patient does not have the disease). While these characteristics are good descriptors of the test’s efficacy, they are less helpful for specific patients.
The mnemonics SpIn and SnOut are often taught to help rationalize the value of these constructs in patients. Thanks to Damien Roland for helping me to further clarify this:
SnOut =
Sensitivity rules Out: When a 100% sensitive test is negative the patient does NOT HAVE the disease.SpIn =
Specificity rules In: When a 100% specific test is positive the patient HAS the disease.
Unfortunately, these mnemonics are only help in 2/4 cases (Negative result on a sensitive test? Rule it SnOut! Positive result on a specific test? Rule it SpIn!). I found myself getting tripped up when a test with low specificity was positive (ie DDimer for PE) or a test with low sensitivity was negative (ie FAST for free fluid). Where do results like this leave us? We can’t rule the disease in or out…
But since when was the world so black and white? When less specific tests are positive or less sensitive tests are negative it still affects the likelihood of the diagnosis. Wouldn’t it be more clinically useful if there was a construct that told us how much more/less probable it was that a patient had the disease? If we could talk about how these results affected clinical likelihood rather than simply if a disease can be ruled in or out?
Fortunately, there is. And I wish I had learned more about it in medical school.
What is more useful: Likelihood Ratios
The statistics gurus came up with a way for us to merge sensitivity and specificity into something that is clinically useful without the need to spIn or snOut. Better yet, using them allows higher level thinking to quantify the new probability of disease based on the pre-test probability of the disease and the test results.
To interpret a positive test you use the positive likelihood ratio (+LR)
+LR = Sensitivity / (1 – Specificity)To interpret a negative test you use the negative likelihood ratio (-LR)
-LR = (1 – Sensitivity) / Specificity
If you are able to estimate the probability of the patient having the disease prior to the test (pre-test probability) you can use a likelihood ratio to determine the post-test probability. A likelihood ratio of 1 means the test does not impact your pretest probability at all. Traditionally, positive and negative likelihood ratios of 10 and 0.1 are considered sufficient to change your pre-test probability enough to affect your decision making. However, the LR’s of most tests are smaller than this and are still helpful clinically to adjust the probability of disease. We often use historical, physical exam, imaging and laboratory “tests” with small-moderate LR’s to determine if there is high enough probability of a diagnosis to move forward down a diagnostic pathway. For example, whether PE is enough of a concern to order a CTPA. This article describes this concept in detail and explains the important concepts of test and treatment thresholds. Bottom line: the size of a LR can be used as a guide to determine how helpful (or unhelpful) a test is.
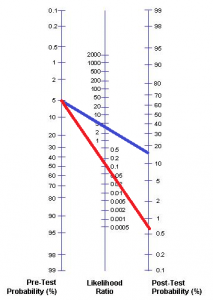
The pretest probability can be combined with a LR to determine the post-test probability with the nomogram below. There are two main ways to estimate pre-test probability. Decision tools (ie Well’s Criteria, PECARN) provide pre-test probabilities based on clinical features while clinical experience allows a clinician to form a “gestalt” impression of how likely it is that a patient has disease. While the latter method is not extraordinarily accurate I think it is acceptable because it is often what we have available most often and what we regularly base our decisions on.
Once we have specified a pre-test probability we can plug it into a Fagan nomogram like the one posted below to calculate the post test probability.
TheNNT is an amazing (and free!) website with a repository of likelihood ratios that can be used in this way.
Example: Aortic Dissection
Say you have a 68 year old patient that presents with chest pain. Before you set foot in the room you have multiple potential diagnoses in mind: MI, pneumonia, pulmonary embolism, aortic dissection, MSK pain, GERD, etc. Each of these conditions have different likelihoods in this patient that you will adjust as you get more information. Aortic dissection is a rare but dangerous condition that it is difficult to distinguish from the others on the list. How likely is it that your patient has that?
In this case, I was unable to find a good pre-test probability (the proportion of patients that present with chest pain that have aortic dissection). However, experience and teaching have informed me that it is very rare so I’ll estimate its initial likelihood in this patient at 1/200 (0.5%). As the history and physical exam continue I will adjust this probability using +/- LR’s.
At some point you will ask him to describe his pain. As it turns out, this is one of the best features for distinguishing the chest pain of aortic dissection from other causes of chest pain. This historical “test” has a +LR of 10.9 and a -LR of 0.3. Using the Fagan nomogram we can determine the likelihood of aortic dissection based on his answer (the test result).
If the patient describes his chest pain as “ripping” his post test probability of aortic dissection increases to ~5% (blue line). If he does not his post-test probability drops to ~0.2% (red line). This test neither ruled in or out the diagnosis but it still contributed to our clinical reasoning. A 5% chance means aortic dissection is still unlikely, but it is now likely enough that you need to test further.
After the CXR comes back you’d likely look closely at the aorta for an enlarged aorta or widened mediastinum. A colleague might criticize you for doing so because “everyone knows that a CXR is not at all specific for aortic dissection.” While they would be correct in their assertion, I would argue that they are wrong in their conclusion. While CXR is poorly specific for dissection, the combination of its sensitivity and specificity are enough to give likelihood ratios (+LR of 3.4 and -LR of 0.13) that may affect care. Pulling out the Fagan Nomogram again:
A positive result increases the post-test probability to ~15% while a negative result reduces it back down to ~0.6%. Call me crazy, but there’s no way I’m letting a patient with a 15% probability of having an aortic dissection leave without ruling it out! While there would be other features to consider, this probability is above the “test threshold” for ordering a CT scan. As for the CXR having no value for aortic dissection, note that the presence/absence of this sign swung the likelihood from as high as 15% to as low as 0.6%. That is relevant to me in this case.
On the other hand, there are times that ordering a CXR would be frivolous. For example, if our patient had sudden onset (+LR 2.6) ripping chest pain (+LR 10.8) that was migrating (+LR 7.6), a pulse differential (+LR 2.7) and a right hemiparesis (+LR between 2 and 549) along with a PMHx of Marfan’s Syndrome (no known LR, but a condition that predisposes to aortic dissection) it would be extremely likely that the patient is having a dissection. In this context, even a negative CXR does not have a high enough -LR (0.13) to lower the risk of the disease low enough to avoid a CT (the probability of aortic dissection would still be above the test threshold!). In this case we should forget the x-ray and urgently order the CT (and call the surgeon!).
Application
You might be thinking that you don’t have time to bust out a nomogram and draw lines on it while you’re working. Neither do I. However, I find knowing approximate likelihood ratios more useful than approximate sensitivity and specificity. LR’s help me to better quantify the size of the effect that a historical, physical or laboratory finding has on the probability of a diagnosis. The ability to quantify probability makes it easier to have conversations with patients in a language they understand. For these reasons I would highly recommend that medical students drop the love-in with SpIn and SnOut and learn more about likelihood ratios. It is important to internalize the approximate likelihood ratios of each diagnostic tool/disease and understand which have sufficient diagnostic accuracy to affect our judgement.
Geek-out: Bayesian Statistics and the Fagan Nomogram
On a historical note, likelihood ratios are a method of applying Bayesian statistics to help us make better clinical decisions.
Bayes was a philosophical Englishman born ~1700 and the granddaddy of probabilistic statistics. His ingenious theorem of conditional probability was published posthumously. While Bayes Theorem looks complicated, it is effectively a formula to take a known probability and modify it based on additional information to come up with a new probability.
The application of likelihood ratios to medical decision making is an elegant use of this theorem. Fagan published the nomogram demonstrated above in the 1975 issue of the NEJM. As demonstrated, it allows us to accurately incorporate test results into a situation to determine the likelihood of a diagnosis.
To learn more about the application of Bayesian statistics in a variety of areas, I highly recommend reading The Signal and the Noise by Nate Silver. It was the reference for this geek-out.
Conclusion
I hope this post gave you a better understanding of diagnostic statistics and convinced you of the superiority of likelihood ratios and Bayesian thinking. If you want to consolidate these principles for yourself I highly recommend doing four things:
Read the excellent articles Likelihood Ratio: A Powerful Tool for Incorporating the Results of a Diagnostic Test into Clinical Decision Making and Diagnostic testing revisited: pathways through uncertainty
Listen to the SMART:EM podcast Testing: Back to Basics
Listen to the SMART:EM podcast SAH: A Picture is Worth a Thousand LP’s (this podcast takes these concepts even further into the calculation and application of test and treatment thresholds)
Read The Signal and the Noise by Nate Silver
Visit TheNNT‘s Likelihood Ratio section for a spectacular repository of relevant LR’s
Thanks to Rory Spiegal who writes at EMNerd for peer reviewing this post. I highly recommend checking out his site – he has been putting out golden analyses of some very difficult EM literature.
Brent Thoma
Latest posts by Brent Thoma (see all)
- We’re hiring a website coordinator! - May 19, 2022
- FRCPC or CCFP-EM: What is best for you? - March 31, 2022
- 2021 CanadiEM Year in Review and Editor’s Choice Awards - January 4, 2022